Merkle Trees

Bitcoin block headers contain a field called the merkle root. The merkle root is a compact cryptographic representation of the transactions contained in the block. To build the tree the transactions are first hashed, then the hashes are paired together, concatenated, and hashed again. This process is repeated for each layer of the tree until you have a single "root" hash at the top of the tree as shown below.

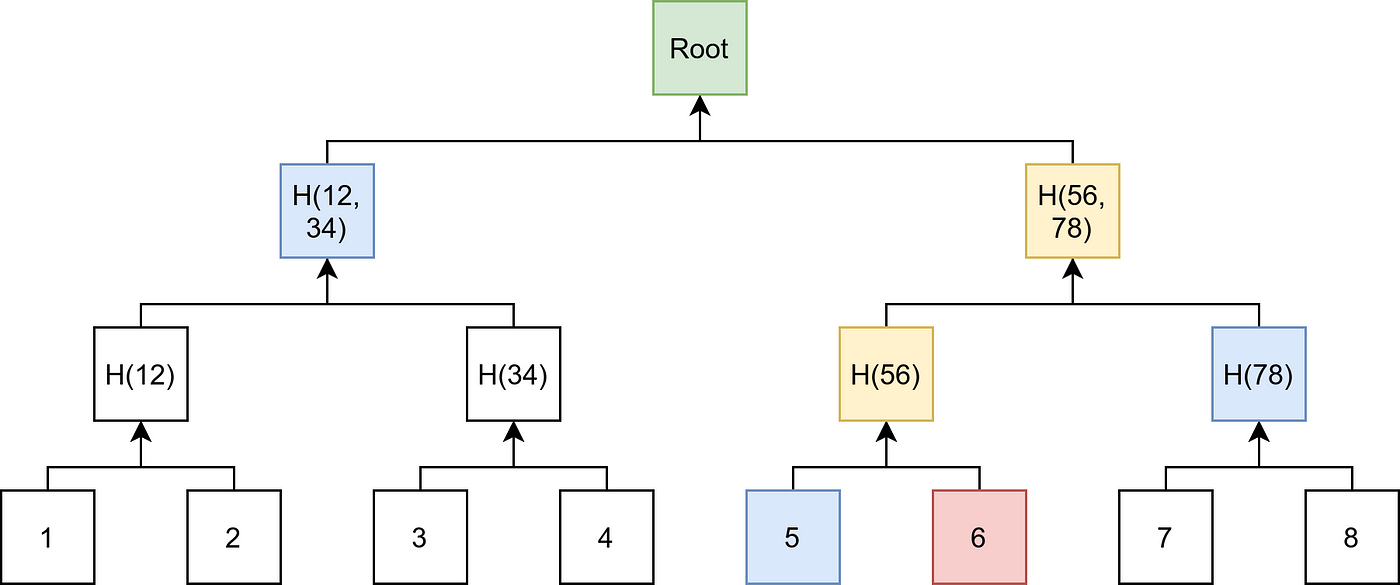
A unique feature of the merkle tree is that it allows us to build compact inclusion proofs. For example, if I want to prove that transaction 6 is in the block, I could do so by providing you with the full list of transactions in the block. That would work, you would see that, indeed, transaction 6 is in the block, but it's not very compact. Especially for larger blocks.

Using the merkle tree we can create a proof that is much more compact. In this case the proof would consist of:

• The hash of transaction 5
• H78
• H1234

From that information a verifier could compute H56, H5678, and the root hash. Then compare the root hash to the hash in the block header.

Illium also uses the exact same merkle tree to represent transactions in the block header, but in addition, at each block we also calculate a merkle root of the entire set of transaction output commitments found in the entire blockchain.

We call this the Txoc Set Root (txoc stands for transaction output commitment).

Recomputing the entire merkle tree every new block would be extremely resource intensive. Even more so when one considers that the size of the txoc set is extremely large. Much larger than the number of transactions in a block.

For this reason we use a variant of the Bitcoin merkle tree that is optimized for appends. We call this tree the Txoc Set Accumulator.

It works as follows. First, when we insert a new output commitment into the tree we prepend it with its index in the tree before hashing:

hash := hash(index, outputCommitment)

This ensures that each hash in the tree is unique, even if the output commitment is not.

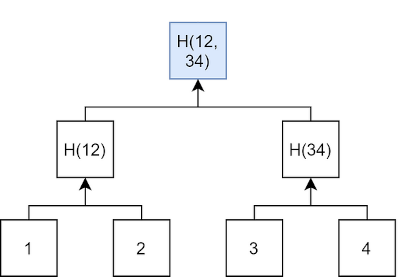
Now suppose we have four output commitments in the tree. It would look just like a normal merkle tree:

If we were to add a fifth output commitment we would simply leave that output loose and treat it as its own separate "peak".

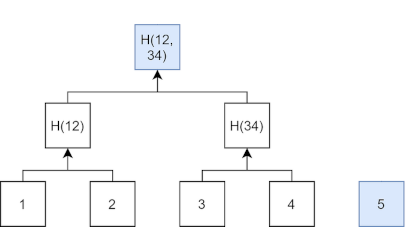
Now we have a tree with two "peaks". We can compute the merkle root for the txoc set as the merkle root of the set of peaks. In this case:

root := hash(peak1, peak2)

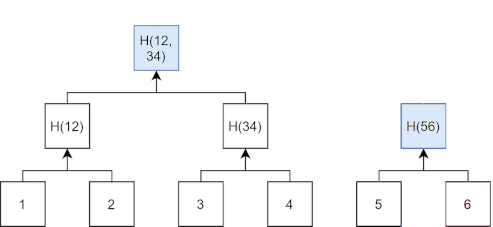
If we add a sixth output commitment the second tree grows in size:

After a seventh output commitment we now have three peaks:

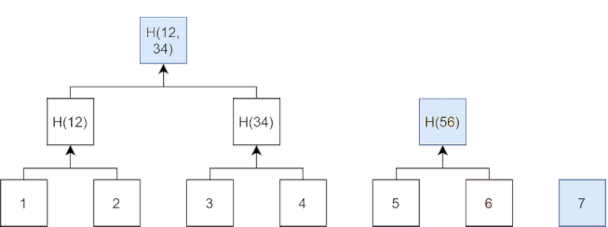
Again, we compute the txoc root by building a regular merkle tree out of the peaks:

h1 := hash(peak1, peak2)
h2 := hash(peak3, peak3) // As in bitcoin, an unpaired element gets hashed with itself.
root := hash(h1, h2)

After adding an eighth output commitment into the tree, all the peaks merge back into a single peak:

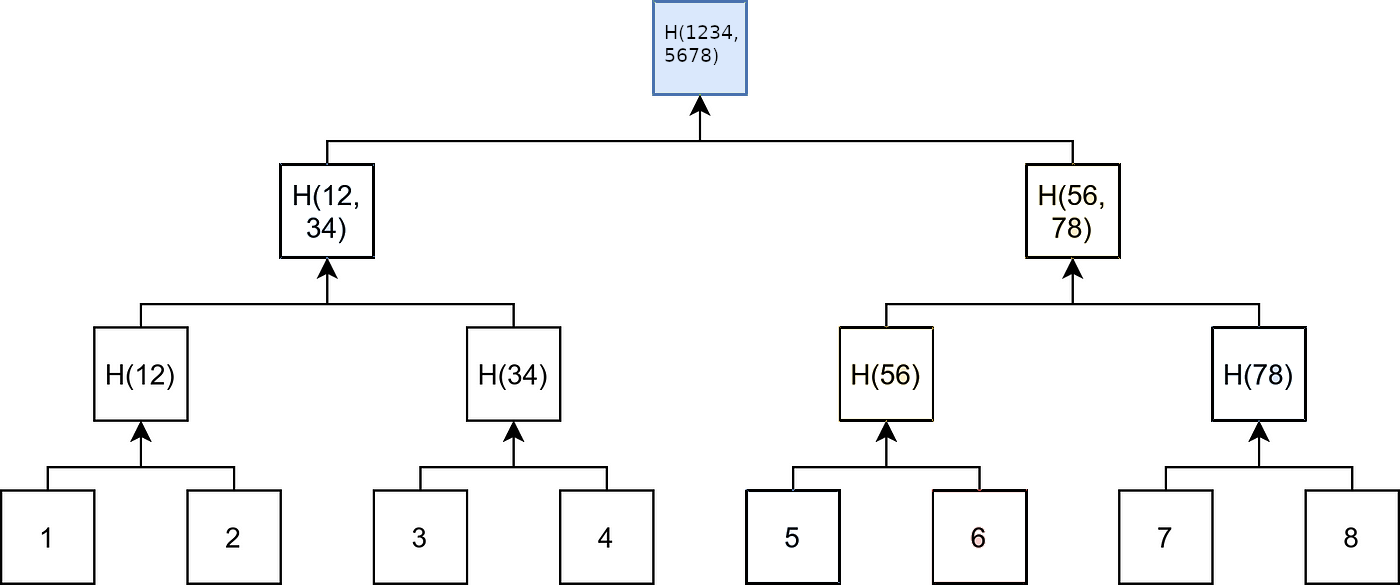
So what we end up with is the number of peaks in the accumulator expands as the number of output commitments grows, but then at some point it collapses back to a single peak. Each round of expansion the number of peaks grows by one. Overall the number of peaks grows logarithmically with the number of output commitments.

Additionally, full nodes only need to store the peaks on disk in order to update the accumulator and all the intermediate branches can be deleted. So this accumulator uses very little disk space and very little CPU to update with each new block.

Just like the original merkle tree, we can still build compact inclusion proofs which we will need later to prove that our transaction inputs are valid.